동전 게임

https://www.acmicpc.net/problem/10837

---

풀이

문제의 규칙에서 1. 항상 영희가 먼저 동전을 던지고,
2. 남은 기회가 있더라도 점수 계산 시 이기지 못한다고 판단되면 중지한다는 것을 유념해야 한다.

문제를 해결한 아이디어는 입력된 점수가 될 수 있는지 판단하기 위해
전 라운드가 성립할 수 있을지를 생각해 보았다.

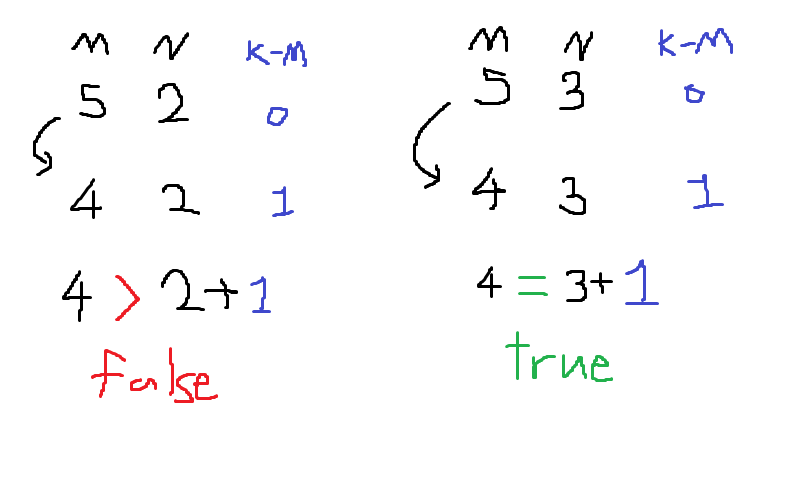
영희와 동수의 점수 중 더 큰값을 현재의 라운드라고 생각할 수 있으며 그 전 라운드는 큰값의 -1한 점수라 생각할 수 있다.
위 그림처럼 영희의 점수(m), 동수의 점수(n)가 '5 2'와 '5 3'으로 주어졌을 때를 생각해보면 그 전라운드는 '4 2'와 '4 3'이다.
'4 2'의 경우 영희가 던질 수 없다. 왜냐하면 동수가 점수를 얻지 못한 시점에서 게임이 종료되기 때문이다.
'4 3'의 경우 영희가 점수를 얻어 '5 3'이 되는 순간 끝나기 때문에 가능하다.
즉 전라운드에서 부터 남은 모든 라운드에 동수가 점수를 얻은 값이 전라운드의 영희의 값보다 크거나 같아야 성립할 수 있다.
때문에 동수의 점수(n) + 전라운드부터 얻을 수 있는 점수(k - (m - 1))가 영희의 전라운드 점수(m - 1)보다 작다면 성립할 수 없다.

동수의 점수가 영희보다 클 경우도 마찬가지로 생각해서 여부를 따질 수 있다.
하지만 다른점은 규칙 1에 의해 영희가 항상 먼저 동전을 던지기 때문에 '1 3'같은 상황이 성립한다.
'1 3'의 전라운드는 '1 2'로 볼 수있으며 영희가 뒷면이 나와 점수 획득을 못해도 동수역수 획득 못할 확률이 있기 때문에
동수가 동전을 던지는 것을 허용하므로 '1 3'이 성립할 수 있다.
즉, 동수는 1의 차이를 더 허용한다.